by
J.C. Pechmann, S.J. Nava, J.C. Bernier, F.M. Terra, and R. Burlacu
December 6, 2006
This report summarizes the procedures currently in use at the University of Utah Seismograph Stations (UUSS) for determining local earthquake magnitudes. It also describes how these procedures have been retroactively applied to improve the magnitude estimates in the UUSS earthquake catalogs for the time period over which the UUSS regional seismic network has been digitally recorded: 1981-present.
UUSS earthquake catalogs for the Utah (UT) and Yellowstone National Park (YP) regions contain two types of size measurements: Richter local magnitude (ML; Richter, 1958, pp. 340-345) and coda magnitude (MC). ML is the preferred size measurement, but cannot be determined for most of the smaller earthquakes in the catalogs. The equations for the MC calculations are calibrated against ML in order to achieve consistency in the two different size estimates. Magnitudes reported in the revised 1981-present catalogs are either ML or MC, as indicated. However, some of the magnitudes in the previous UT catalog for the time period 1981 to April 1994, and in the current 1962-1980 UT catalog, are averages of MLs and MCs.
Local Magnitudes
The MLs are calculated from maximum amplitudes measured either on paper records from Wood-Anderson (W-A) short-period seismographs or else on synthetic W-A records. Synthetic W-A records are digital records that have been processed to be equivalent to paper records from W-A seismographs (see Bakun et al., 1978; Kanamori and Jennings, 1978). For earthquakes from May 1979 through 1993, the amplitude measurements for UUSS MLs are from paper records from two W-A seismographs in Utah (at DUG and SLC). For earthquakes since 1994, the MLs have been determined primarily using synthetic W-A records from 27 UUSS and nearby U. S. National Seismic Network (USNSN) broadband digital telemetry stations (Table 1).
UUSS MLs have been calculated using Richter’s (1935, 1958) definition and distance corrections since at least 1962:
ML = log10 A – log10 A0 + Si (1)
where
A = the maximum trace amplitude in millimeters on a W-A record,
log A0 = an empirical distance correction from Richter (1958), and
Si = an empirical correction for the particular station and/or instrument used.
At UUSS, the maximum trace amplitude used in (1) is the mean of half the maximum peak-to-peak amplitudes measured on the two horizontal-component W-A records. Currently, ML determinations from two or more stations are averaged to obtain the ML value for an earthquake.
Table 1: Local Magnitude Station Corrections+
| Station Code | Instrument Type* | Station Correction, Si (sec) | Std. Dev. of Si, s(Si)(sec) | Number of Measurements | Date Implemented (mm/dd/yyyy)# |
| AHID | BB | -0.43 | 0.04 | 83 | |
| BGU | BB | +0.03 | 0.07 | 15 | |
| BOZ | BB | +0.17 | 0.04 | 14 | 06/01/2004 |
| BUT | W-A | -0.23 | 0.08 | 17 | |
| BW06 | BB | -0.15 | 0.04 | 69 | |
| CTU | BB | +0.10 | 0.02 | 234 | |
| DUG-paper§ | W-A | +0.20 | — | — | |
| DUG-digital | BB | +0.08 | — | — | |
| ELK | BB | +0.02 | 0.07 | 10 | |
| GOL‡ | BB | -0.36 | 0.01 | 64 | |
| HLID | BB | +0.05 | 0.07 | 14 | |
| HVU | BB | -0.21 | 0.02 | 164 | |
| HWUT | BB | +0.09 | 0.03 | 124 | |
| IRCI‡ | BB | +0.05 | 0.03 | 80 | |
| JLU | BB | +0.05 | 0.06 | 15 | |
| KNB | BB | +0.21 | 0.03 | 86 | |
| LDS | BB | -0.26 | 0.05 | 31 | |
| LKWY | BB | +0.06 | 0.07 | 23 | |
| MPU | BB | +0.20 | 0.02 | 211 | |
| MVU | BB | -0.11 | 0.04 | 91 | |
| NLU | BB | +0.14 | 0.04 | 23 | |
| NOQ | BB | -0.08 | 0.02 | 164 | |
| SLC ¶ | W-A | -0.21 | 0.05 | 56 | |
| SPU | BB | -0.10 | 0.05 | 46 | 07/01/2003 |
| SRU | BB | -0.35 | 0.02 | 259 | |
| TCU | BB | -0.55 | 0.04 | 58 | 07/01/2003 |
| TMU, TM2 | BB, SP | -0.28 | 0.04 | 56 | 07/01/2003 |
| TPNV | BB | -0.22 | 0.07 | 10 | 07/01/2003 |
| YFT | BB | +0.20 | 0.05 | 12 | 06/01/2004 |
| YMR | BB | -0.38 | 0.07 | 15 | |
| + From Pechmann et al. (2007), except for the entries in italics* BB = broadband, W-A = Wood-Anderson, SP = short period# If a date is given, the station was used for ML calculations only for earthquakes after this date
§ Station correction taken from Griscom and Arabasz (1979) ‡ Developed for and applied only to earthquakes which occurred during 1994 in the Draney Peak, Idaho, region (between the UT and YP catalog regions): 42º 30´- 43º 10´ N, 110º 40´- 111º 35´ W ¶ Station correction derived from paper record data but applied to magnitudes from both paper and digital records for earthquakes after July 10, 1985, when the SLC W-A instrument was rebuilt; for earlier events, Griscom and Arabasz’s (1979) station correction of 0.0 is used |
|||||
Pechmann et al. (2000, 2007) showed that Richter’s (1958) distance corrections are adequate for use in the region spanned by the UUSS regional seismic network. They also developed empirical ML station corrections for 21 stations in this area (Table 1, entries in regular type) and used them in equation (1) to recompute all MLs in the UUSS earthquake catalogs from 1981-2002. Station corrections for eight other stations have been developed using the same methodology (Table 1, entries in italics). Data from two of these eight stations have been used in ML determinations only on a restricted basis (see Table 1 footnotes). Data from the other six stations have been used in ML determinations only for earthquakes that occurred after the corrections were determined and implemented (dates, Table 1).
The station corrections minimize differences between MLs calculated from different stations and from paper and synthetic W-A records. For all of the stations except DUG, chosen as the reference station because of its long recording history with both W-A and broadband seismometers, the station corrections were calculated as follows:
Si = ML (DUG-digital) – ML(i) (2)
where the overbar indicates the mean value, ML(i) is the uncorrected ML from station i, and ML(DUG-digital) is the ML from the DUG synthetic W-A records, after applying the station correction of +0.08 (Table 1). See Pechmann et al. (2007) for further details and explanation.
Coda Magnitudes
The MCs are calculated from measurements of seismic signal durations on records from short-period, vertical-component, velocity sensors. For the 1981 through 2000 earthquake catalogs, almost all of the MCs were originally determined from digital records using the following equations (Griscom and Arabasz, 1979; Smith et al., 1986):
MC = -3.13 + 2.74 log τ + .0012Δ in the UT region, (3)
MC = -2.25 + 2.77 log τ + .0030Δ in the YP region, (4)
where Δ = epicentral distance in km,
τ = signal duration in sec, measured from the P-wave onset to the time that the signal drops down below the pre-event noise level.
MC determinations from several stations were usually averaged to obtain the MC value for an earthquake. A few of the MCs in the original 1981-1983 UT region catalog (Richins et al., 1984) were determined using paper records from a Benioff seismograph at DUG and the following equation (Griscom and Arabasz, 1979):
MC = -4.26 + 2.79 log τ + .0026Δ , (5)
where Δ and τ have the same definitions as above.
Unfortunately, there were systematic time-dependent differences between the MCs computed using equations (3) and (4) and MLs computed using (1). These differences ranged up to 0.4 and 0.9 units in the UT and YP regions, respectively. Pechmann et al. (2000, 2001) showed that these differences were primarily due to inaccuracies in the MCs caused, in part, by the effects of varying instrument gains and background noise levels on the signal duration measurements. They solved this problem by redefining the signal duration in terms of absolute ground motion levels and revising the coda magnitude equations.
Since 2002, UUSS MCs have been calculated from digital records using the following equations updated from Pechmann et al. (2001):
MC = -2.25 + 2.32 log τ + .0023Δ in the UT region, (6)
MC = -2.60 + 2.44 log τ + .0040Δ in the YP region, (7)
where Δ = epicentral distance in km,
τ = signal duration in sec, measured from the P-wave onset to the time that the average absolute value of the ground velocity (approximated from the record amplitudes and the 5 Hz instrument gain) drops below 0.01724 microns/sec.
The MCs for the 2001 catalogs, and for some mining-related events during the last quarter of 2000, were originally computed using the new τ definition but earlier versions of the above equations. The threshold of 0.01724 microns/sec in the new τ definition is the estimated median noise level for short-period analog-telemetry stations in the University of Utah regional seismic network (as of August 1, 2000).
Equation (6) was calibrated against MLs for 923 Utah region earthquakes of ML 0.5 to 4.7 which occurred between 1983 and 2001. Equation (7) was calibrated against MLs for 510 Yellowstone region earthquakes of ML 0.6 to 4.2 which occurred between 1995 and 2001. To determine the constants in the MC equations, we used an orthogonal regression method (Cheng and Van Ness, 1999, pp. 9-11) rather than linear regression. The latter produces biased results because the errors in the predictor variables (log τ and Δ) are not negligible compared to the errors in the response variable (ML) (see Draper and Smith, 1981, pp. 122-125). The coda magnitudes provided by equations (6) and (7) are comparable to local magnitudes over the range of applicability of these equations, which we consider to be 0.5 ≤ ML ≤ 5 (Figure 1). The finite record lengths of UUSS recording system triggers appear to have caused underestimation of signal durations for earthquakes of ML > 5 (Figure 1a, crosses).
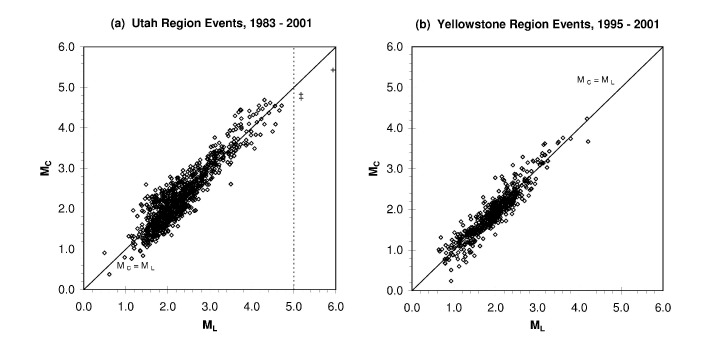
Figure 1. Plots of MC versus ML for (a) the 923 Utah region earthquakes used to determine equation (6) (diamonds) and (b) the 510 Yellowstone region earthquakes used to determine equation (7). The coda magnitudes were calculated using equations (6) and (7), respectively. The solid line marks the line of perfect agreement: MC = ML . The dotted line on (a) separates data points that were used (diamonds) and not used (crosses) in the regression.
Most of the τ measurements since mid-1987 have been made with the aid of UUSS-developed software that automatically determines signal duration from a user-selected portion of the coda—the latter part of the seismic record where the amplitude is decaying with time. The code determines the average absolute value, A, of the de-meaned digital seismogram in overlap-ping 2-sec time windows space 1 sec apart. It then fits the A values with a function of the form:
A(t) = A0 (t – tp)-α (8)
where t = time,
tp = P-wave arrival time, and
A0, α = constants.
The end of the signal is initially defined as the intersection between A(t) and a threshold of 5.0 digital counts. This threshold matches the ground velocity threshold of 0.01724 microns/sec in (6) and (7) for an instrument with a gain of 290 counts/(micron/sec). Let τ5 be the observed signal duration measured to the 5-count threshold. τ5 is converted to τ, as part of the MC calculation procedure, by correcting for the actual instrument gain (at 5 Hz) using the following equation derived from (8):
τ = τ5 (Gs /G)1/α (9)
where Gs = 290 counts/(micron/sec) = “standard” instrument gain at 5 Hz, and
G = actual instrument gain at 5 Hz
This gain correction method was experimentally verified by Pechmann et al. (2000). The median value for α, 1.8, is used for the gain correction in cases where the signal duration was picked manually.
Revision of UUSS Magnitudes, 1981-2001
The revised MLs from Pechmann et al. (2007) have been incorporated into the 1981-2001 UUSS earthquake catalogs. The changes to the existing MLs resulted primarily from using the new station corrections and applying the requirements that: (a) all reported MLs be average ML values from two or more stations and (b) only maximum peak-to-peak amplitudes of 1.0 mm or greater from paper records be used. An exception to (a) was made for the February 3, 1994, MW 5.7 Draney Peak, Idaho main shock, which was located between the Utah and Yellowstone regions. For this earthquake, we reported a single-station ML of 5.9 from DUG because that was the only magnitude estimate we could determine for it. An exception to (b) was made for the smaller earthquakes in the 1994 Draney Peak sequence, for which we used some peak-to-peak amplitudes of < 1 mm from DUG paper records.
For the time period January 1981 through April 1994, the old UT catalog had 442 “Wood-Anderson” magnitudes whereas the new UT catalog has only 47. The main reason for this difference is that most of the “Wood-Anderson” magnitudes in the old catalog were single station MLs or averages of single station MLs and MCs from Benioff seismograph paper records (Richins et al., 1984; Brown et al., 1986; Nava et al., 1990). The Benioff MCs were calculated from equation (5) using data from stations CCU (January through April, 1981) and DUG (January 1981 to April 8, 1994). The “Wood-Anderson” magnitudes in the new catalogs, on the other hand, are all MLs determined from peak amplitudes on Wood-Anderson records using the methods and criteria described herein. The revised 1981-2001 catalogs do not include any MCs determined from Benioff paper records or any ML–MC averages. Note that for the time period May 1994 through December 2001, MLs had been previously reported for only a handful of the 1393 earthquakes for which there are MLs in the revised UT and YP catalogs (except for the MLs published in the electronic supplement to Pankow et al., 2004).
We recomputed all of the MCs in the 1981-2001 UUSS earthquake catalogs using our current methods. The changes to the MCs resulted primarily from the application of the new MC equations (6) and (7), along with the revised signal duration definition. Some changes to the MCs also occurred because we modified our version of the earthquake location program Hypoinverse (Klein, 1978) to compute and report negative magnitudes instead of discarding them. (We also changed the default magnitude from 0.00 to –9.99.)
The gain correction factor for the signal durations is sensitive to the coda decay parameter, α, because of the 1/α exponent in equation (9). This sensitivity, combined with uncertainties in α and limitations of the coda decay model (8), can sometime lead to erroneous coda magnitudes. Because of this problem, we removed all MC values that differed from the mean for the earthquake by more than 1.0 units. This process was done iteratively, one value at a time, beginning with the largest outlier and recomputing the mean MC after every removal. As this method of identifying outliers does not work for earthquakes with less than three duration measurements, we measured additional signal durations for 4,238 earthquakes having less than three such measurements from stations with known gains. We tried unsuccessfully to measure additional signal durations for nearly 1,500 other earthquakes.
Finally, we carried out some quality control checks on the revised MCs, including those for earthquakes outside the UT and YP regions. One of the primary checks was to compare the revised MCs to the magnitudes (MC or ML ) in the old UUSS catalogs. Based on the distribution of these magnitude differences, we checked and revised, as necessary, all 861 of the new MCs (1.7%) that differed from the old magnitudes by 1.0 units or more. Because there were large systematic errors (up to 0.9 units) in the old Yellowstone MCs (Pechmann et al., 2001), we checked the revised Yellowstone MCs against a catalog containing MLs plus MCs calculated using the old Utah MC equation (3). The magnitudes in the revised UUSS catalogs should be significantly more homogenous and reliable than those in the old catalogs.
Acknowledgments
George Peter Fivas, Kris Pankow, Salah Mehanee, and Ali Moeinvaziri wrote some of the computer codes used in the magnitude revision project. The tedious work of repicking the signal duration measurements was done primarily by Paul Roberson, with help from Jeff Fotheringham, Jane Hoffman, and Mark Hale. We thank Walter Arabasz and Kris Pankow for helpful discussions and for their comments on this report. This work was supported by the USGS, Department of the Interior, under USGS award numbers 98HQAG01939, 01HQAG0014 and 04HQAG0014, and by the State of Utah under a line-item appropriation to the University of Utah Seismograph Stations.
References
Bakun, W. H., S. T. Houck, and W. H. K. Lee (1978). A direct comparison of “synthetic” and actual Wood-Anderson seismograms, Bull. Seism. Soc. Am. 68, 1199-1202, doi:10.1785/BSSA0680041199.
Brown, E. D., W. J. Arabasz, J. C. Pechmann, E. McPherson, L. L. Hall, P. J. Oehmich, and G. M. Hathaway (1986). Earthquake Data for the Utah Region, January 1, 1984 to December 31, 1985, Special Publication, University of Utah Seismograph Stations, Salt Lake City, Utah, 83 pp.
Cheng, C., and J.W. Van Ness (1999). Statistical Regression with Measurement Error, Oxford University Press, New York, New York, 262 pp, ISBN: 978-0-470-71106-4.
Draper, N.R., and H. Smith (1981). Applied Regression Analysis (Second Edition), John Wiley and Sons, New York, New York, 709 pp, ISBN: 0471170828, 9780471170822.
Griscom, M. and W. J. Arabasz (1979). Local magnitude (ML) in the Wasatch Front and Utah region: Wood-Anderson calibration, coda-duration estimates of ML , and ML versus Mb , in Earthquake Studies in Utah, 1850 to 1978, W. J. Arabasz, R. B. Smith, and W. D. Richins (Editors), Special Publication, University of Utah Seismograph Stations, Salt Lake City, Utah, 433-443.
Kanamori, H., and P. C. Jennings (1978). Determination of local magnitude, ML, from strong-motion accelerograms, Bull. Seism. Soc. Am. 68, 471-485, doi:10.1785/BSSA0680020471.
Klein, F.W. (1978). Hypocenter location program HYPOINVERSE, U.S. Geol. Surv. Open-File Rept. 78-694, 113 pp, doi:10.3133/ofr78694.
Nava, S. J., J. C. Pechmann, W. J. Arabasz, E. D. Brown, L. L. Hall, P. J. Oehmich, E. McPherson, and J. K. Whipp (1990). Earthquake Catalog for the Utah Region, January 1, 1986 to December 31, 1988, Special Publication, University of Utah Seismograph Stations, Salt Lake City, Utah, 96 pp.
Pankow, K.L., W.J. Arabasz, J.C. Pechmann, and S.J. Nava (2004). Triggered seismicity in Utah from the 3 November, 2002, Denali fault earthquake, Bull. Seism. Soc. Am. 94, S332-S347, doi:10.1785/0120040609.
Pechmann, J. C., S. J. Nava, J. C. Bernier, and W. J. Arabasz (2000). A critical analysis of systematic time dependent coda magnitude errors in the University of Utah earthquake catalog, 1981 1999, EOS, Trans. Am. Geophys. Union 81, no. 48 (Supplement), F869.
Pechmann, J. C., J. C. Bernier, S. J. Nava, F. M. Terra, and W. J. Arabasz (2001). Correction of systematic time dependent coda magnitude errors in the Utah and Yellowstone National Park region earthquake catalogs, 1981 2001, EOS, Trans. Am. Geophys. Union 82, no. 47 (Supplement), F809.
Pechmann, J. C., S .J. Nava, F. M. Terra, and J. C. Bernier (2007). Local magnitude determinations for Intermountain Seismic Belt earthquakes from broadband digital data, Bull. Seism. Soc. Am., 97 (2): 557-574, doi:10.1785/0120060114.
Richins, W. D., W. J. Arabasz, G. M. Hathaway, E. McPherson, P. J. Oehmich, and L. L. Sells (1984). Earthquake Data for the Utah region, January 1, 1981 to December 31, 1983, Special Publication, University of Utah Seismograph Stations, Salt Lake City, Utah, 111 pp.
Richter, C. F. (1935). An instrumental earthquake magnitude scale, Bull. Seism. Soc. Am., 25 (1), 1-32, doi:10.1785/BSSA0250010001.
Richter, C. F. (1958). Elementary Seismology, W.H. Freeman and Co., San Francisco, California, 768 pp.
Smith, R. B., W. C. Nagy, E. McPherson, I. T. Bjarnason, E. D. Brown, L. L. Sells, and R. A. Hutchinson (1986). Earthquake Data for the Yellowstone National Park region, January 1, 1985 to December 31, 1985, Special Publication, University of Utah Seismograph Stations, Salt Lake City, Utah, 68 pp.
